algo-aha

构造笛卡尔树

• https://leetcode.com/problems/maximum-binary-tree/

以数组最大值作根、左边最大值作左子节点、右边最大值作右子节点，如此递归构造的树叫做笛卡尔树。

TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
    // 以最大值为根构造二叉树，正好对应问题"找下一个更大数"
    // 从左往右扫描，当前数num>stk.top()时弹栈顶。
    // 1. 最后的弹出数是num左边<num的最大数，是num的左子节点；
    // 2. 新栈顶是num左边>num的最小数，
    //    => num是新栈顶右边<新栈顶的最大数，是新栈顶的右子节点。
    // 最后，找下一个更大的数 => 留下递减栈 => 最大值在stk[0]
    vector<TreeNode *> stk;
    for (int num : nums) {
        auto curr = new TreeNode(num);
        while (!stk.empty() && num > stk.back()->val) {
            curr->left = stk.back();
            stk.pop_back();
        }

        if (!stk.empty()) stk.back()->right = curr;
        stk.push_back(curr);
    }
    return !stk.empty() ? stk.front() : NULL;
}

下图示例，已构造好子问题[10 8 6 4]，再插入个7：

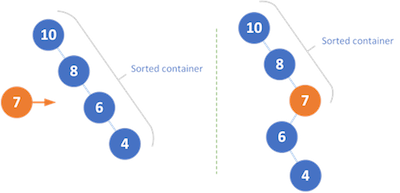
另：若改成留下递增栈，则构造的是以子段最小值为根的笛卡尔树。